Table of Contents
Unified Clear-Sky Solar output Prediction Model
Using the sun as a sustainable energy source isn't really a new invention. Plants have been relying on it for millions of years and have developed and optimized the process of photosynthesis over a very long bio-evolutionary period. Almost everybody appreciates the comfort, when it's warm and the sun is shining but we very often forget how hard our ability to actually survive as a species, is linked to solar output:
Natural interdependently balanced processes
| Global freshwater distribution | Oceans → Evaporate (Desalinize) → Clouds → Rain |
| Global atmospheric conditions (Weather) → | Flora/Fauna (direct) |
| Global Flora → | Food for Fauna (direct) |
| Global atmospheric conditions (Weather) (indirect) |
Technical processes
| Usage | Technology | Result |
|---|---|---|
| Industrial Agriculture | Photosynthesis | Energy (Food) |
| Solar Heating | Mirror/Focus/Transfer | Energy (Thermal) |
| Photovoltaic | Direct, solid-state Photon to Electron conversion | Energy (Electricity) |
Therefore knowledge about global solar radiation (Rs) is of fundamental importance for human life on earth in general and for this project to predict how much Solar (PV) energy we can harvest at any given deployment site in particular, so we depend very much on knowing how much solar energy can be harvested as a clear-sky day maximum, for a specific location on our planet's surface.
Yet we still commonly refer and are taught to use 1000 W/m2 on any point on Earth, as a clear-sky reference value. Even the Watt-Peak value, PV-Panel manufacturers put into their datasheets, is virtually always based only on 1000 W/m2. But how do we actually calculate the output we may generate with a given surface/technology, if we don't know what our clear-sky (Rs)max for a specific location and time will be?

The UCSSPM is an open-source clear-sky prediction model, incorporating math algorithms based on latest research by the Environmental and Water Resources Institute of the American Society of Civil Engineers and a few veteran but still valid and publicly available NOAA/NASA computations and some revised research & assumptions regarding commonly used constants.
With help of this open-source model, anyone can now easily estimate the maximum global solar radiation value on a clear-sky day for any given time and place on Earth - to predict the maximum usable output a given conversion process (currently only PV) may yield. This enables us to plan, calculate, dimension, optimize and control/verify any solar energy conversion system with base data that is as accurate and reliable as possible.
Use-Cases
Photovoltaic Systems
- Estimate the maximum clear-sky PV output for any given site/time/system
- Keep PV panels at optimum elevation without a separate optical solar tracker
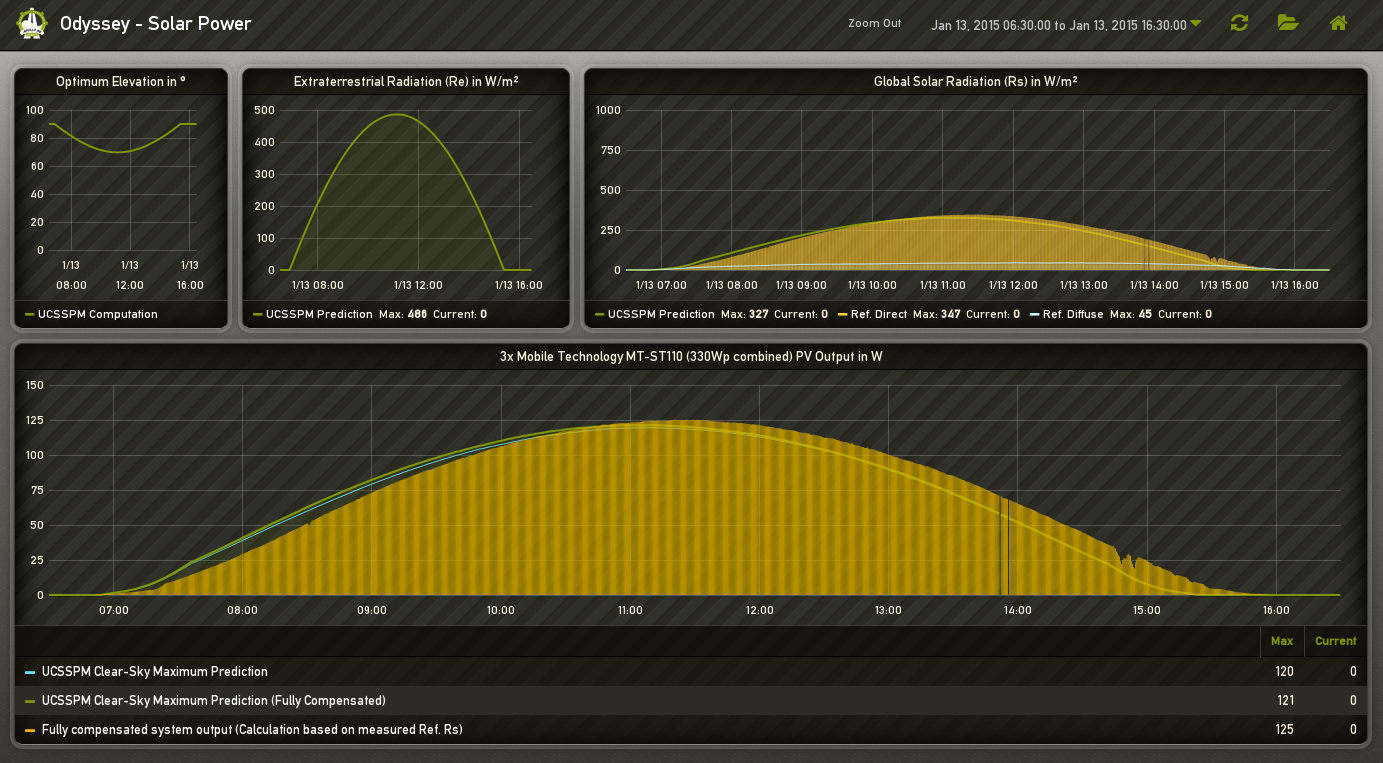
The first full clear sky day since the beginning of data collection has been on 2015-01-13 and the prediction results definitely look very promising as we can see on the following dashboard screenshot:
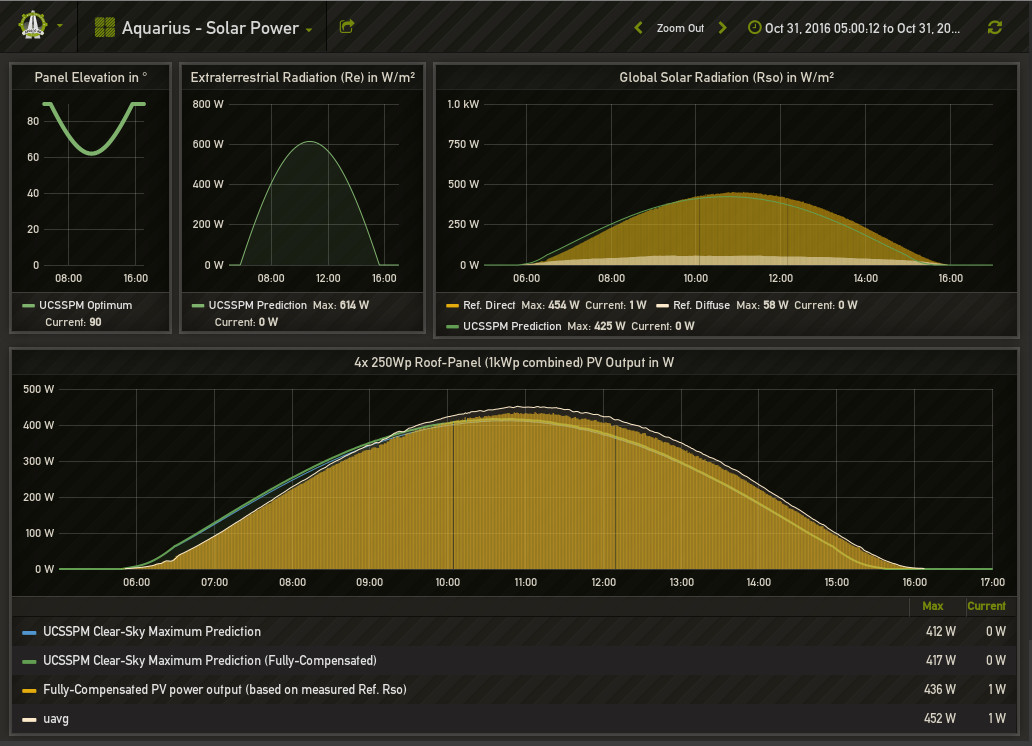
Another random screenshot from 2016-10-31:
Long term PV (live & UCSSPM) metrics are collected and accessible on these VFCC dashboards:
Solar-Ovens
The system can be easily extended to estimate the optimum parabolic oven-reflector size, to satisfy the energy needs for a given project and the specific position on the planet.
Sensor Calibration Reference Model
Possibility to calibrate a Pyranometer in the field, without another calibrated reference, on a clear-sky day.
Agricultural
Usable as basis for open agricultural applications (growth/photosynthetic calculations)
Code
What started out of the necessity to calculate and verify the solar power requirements and project feasibility of Apollo-NG itself, has become an advanced clear-sky prediction model, implemented in python without any further dependency, incorporating the following factors:
- Revised Solar Constant
- Position on Earth
- Day of Year
- Time of Day
- Distance Sun-Earth
- Angle through Atmosphere
- Precipitable water in Atmosphere
- Atmospheric turbidity (Smog, Dust, Air-traffic etc.)
- Direct/diffuse beam radiation
- PV-Panel Surface/Type/Temperature/Age
#!/usr/bin/env python2
# -*- coding: UTF-8 -*-
################################################################################
#
# @file ucsspm.py
# @authors chrono
# @version V1.0.3 (Argument Tamer)
# @date 2014-11-15
# @brief Unified Clear-Sky Solar output Prediction Model (UCSSPM)
# @status Beta - Request for Comment, Re-Verification & Enhancement
#
################################################################################
# Copyright (c) 2014 Apollo-NG - https://apollo.open-resource.org/
################################################################################
#
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 3 of the License, or
# (at your option) any later version.
#
# This program is distributed in the hope that it will be useful,
# but WITHOUT ANY WARRANTY; without even the implied warranty of
# MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
# GNU General Public License for more details.
#
# You should have received a copy of the GNU General Public License
# along with this program. If not, see <http://www.gnu.org/licenses/>.
#
################################################################################
import sys, argparse, math, time, calendar
################################################################################
## Inputs & Defaults #########################################################
################################################################################
def options(arg):
arg.add_argument( "-v", "--verbose" ,\
action = "store_true" ,\
help = "Verbose output" )
# Decreased Solar Constant - See docs/solar-constant.pdf for update info. ##
# Default value of 1361.0 should IMHO serve as a good average point
# between the min/max values over the 11-year sun cycle.
arg.add_argument( "-sc" ,\
type = float ,\
help = "Solar Constant (@1AU) in kW/m² [Default: 1361.0]" ,\
default = 1361.0 )
# Space/Time Pinpointing ###################################################
arg.add_argument( "-lat" ,\
type = float ,\
help = "Latitude in decimal degrees [Default: 48.0]" ,\
default = 48.00000 )
arg.add_argument( "-lon" ,\
type = float ,\
help = "Longitude in decimal degrees [Default: 11.0]" ,\
default = 11.00000 )
# Optional, only needed if barometric pressure not available to compute it.
# If no value is supplied to either, an altitude of 0m (NN) will be default
# Obviously, this is only a fallback and using the actual barometric pressure
# should always be preferred to yield a less averagish result.
arg.add_argument( "-alt" ,\
type = float ,\
help = "Altitude in meters above NN [Default: 0]" ,\
default = 0 )
arg.add_argument( "-date" ,\
type = str ,\
help = "ISO Date YYYY-MM-DD [Default: " \
+ time.strftime("%Y-%m-%d") + "]" ,\
default = time.strftime("%Y-%m-%d") )
arg.add_argument( "-time" ,\
type = str ,\
help = "ISO Time HH:MM:SS [Default: " \
+ time.strftime("%H:%M:%S") + "]" ,\
default = time.strftime("%H:%M:%S") )
# Environmental Conditions #################################################
arg.add_argument( "-at_t" ,\
type = float ,\
help = "Atmospheric Temperature in °C [Default: 25.0]" ,\
default = 25.0 )
arg.add_argument( "-at_h" ,\
type = float ,\
help = "Atmospheric Relative Humidity in Percent [Default: 50]" ,\
default = 50.0 )
# Can be optional by submitting altitude - but will be less precise then ###
arg.add_argument( "-at_p" ,\
type = float ,\
help = "Atmospheric Air Pressure in hPa [Default: Computed]" )
arg.add_argument( "-at_tc" ,\
type = float ,\
help = "Atmospheric Turbidity Coefficient [Default: 0.95]" ,\
default = 0.95 )
# Photovoltaic Parameters ##################################################
arg.add_argument( "-pv_a" ,\
type = float ,\
help = "Effective PV Panel Surface in m² [Default: 1.67]" ,\
default = 1.67 )
arg.add_argument( "-pv_e" ,\
type = float ,\
help = "PV Panel Efficiency in Percent [Default: 16]" ,\
default = 20 )
arg.add_argument( "-pv_t" ,\
type = float ,\
help = "PV Panel Temperature in °C [Default: 25.0]" ,\
default = 25.0 )
arg.add_argument( "-pv_tc" ,\
type = float ,\
help = "PV Panel negative Temp. Coefficient [Default: 0.35]" ,\
default = 0.35 )
arg.add_argument( "-pv_ac" ,\
type = float ,\
help = "PV Panel age related Coefficient [Default: 0.98]" ,\
default = 0.98 )
################################################################################
## Outputs ###################################################################
################################################################################
def output(opt,res):
if res['sol_z'] > 90:
if opt.verbose:
print "The sun has set - no data"
return 0
else:
print "0.0|0.0|90.0|0.0|0.0"
return 0
elif not opt.verbose:
print "%.1f|%.1f|%.1f|%.1f|%.1f" % \
( \
res['ETR'], res['RSO'], res['sol_z'] ,\
res['pv_max'], res['pv_out'] \
)
return 0
else:
print "--------+--------------------------------------------------------"
print " UCSSPM | Clear-Sky Prediction for %s @ %s" % (opt.date, opt.time )
print "--------+--------------------------------------------------------"
print " Solar Constant : %s kW/m² @ 1AU" % opt.sc
print " Atmospheric turbidity coefficient : %s" % opt.at_tc
print "-----------------------------------------------------------------"
print " Equation of time : %s min" % res['eqt']
print " Inverse relative distance factor : %s" % res['sol_r']
print " Sun declination : %s°" % res['sol_d']
print " Solar Noon : %s " % res['sol_n']
print " Barometric Pressure at site : %s kPa" % opt.at_p
print " Estimated Vapor Pressure at site : %s kPa" % res['at_vp']
print " Estimated Extraterrestrial Radiation : %s W/m²" % res['ETR']
print " Estimated precipitable water in Atmosphere : %s mm" % res['at_pw']
print " Clearness index for direct beam radiation : %s" % res['CIDBR']
print " Transmissivity index for diffuse radiation : %s" % res['TIDR']
print "-----------------------------------------------------------------"
print " Estimated Max. global solar radiation (Rs) : \033[1;33m%3.1f W/m²\033[0m" % res['RSO']
print "-----------------------------------------------------------------"
print " Optimum Elevation of PV-Panel : \033[1;37m%02.1f°\033[0m" % res['sol_z']
print " Estimated Max. Clear-Sky PV-Power Output : \033[1;32m%3.1f W\033[0m \033[1;37m@ %d%% Peff\033[0m" % (res['pv_max'], opt.pv_e)
if res['pv_lp'] >= 0:
print " PV-Panel temperature (%2.1f °C) compensation - \033[1;31m%2.1f W / %2.1f%%\033[0m" % (opt.pv_t, res['pv_lp'] , res['pv_l'] )
else:
print " PV-Panel temperature (%2.1f °C) compensation + \033[1;32m%2.1f W / %2.1f%%\033[0m" % (opt.pv_t, res['pv_lp']*-1 , res['pv_l']*-1 )
print " PV-Panel aging loss - \033[1;31m%03.1f W\033[0m" % res['pv_la']
print "-----------------------------------------------------------------"
print " Compensated Max. Clear-Sky PV-Power Output : \033[1;32m%3.1f W\033[0m" % res['pv_out']
return 0
################################################################################
## MAIN ######################################################################
################################################################################
def main():
arg = argparse.ArgumentParser()
options (arg)
opt = arg.parse_args()
parse_d = opt.date.split("-")
opt.year = int(parse_d[0])
opt.month = int(parse_d[1])
opt.day = int(parse_d[2])
parse_t = opt.time.split(":")
opt.hour = int(parse_t[0])
opt.min = int(parse_t[1])
opt.sec = int(parse_t[2])
dst_off = 0
tz_off_deg = 0 + opt.lon
res = {}
# Compute Julian Day (Day of Year) #########################################
if calendar.isleap(opt.year):
# Leap year (366 days)
lMonth = [0,31,60,91,121,152,182,213,244,274,305,335,366]
else:
# Normal year (365 days)
lMonth = [0,31,59,90,120,151,181,212,243,273,304,334,365]
res['DoY'] = lMonth[opt.month - 1] + opt.day
res['ToD'] = float(opt.hour + (opt.min/60.0) + (opt.sec/3600.0))
# Solve equation of time ###################################################
# (More info on http://www.srrb.noaa.gov/highlights/sunrise/azel.html)
res['eqt'] = (((5.0323-(430.847*math.cos((((2*math.pi)*res['DoY'])/366)+4.8718)))\
+ (12.5024*(math.cos(2*((((2*math.pi)*res['DoY'])/366)+4.8718))))\
+ (18.25*(math.cos(3*((((2*math.pi)*res['DoY'])/366)+4.8718))))\
- (100.976*(math.sin((((2*math.pi)*res['DoY'])/366)+4.8718))))\
+ (595.275*(math.sin(2*((((2*math.pi)*res['DoY'])/366)+4.8718))))\
+ (3.6858*(math.sin(3*((((2*math.pi)*res['DoY'])/366)+4.871))))\
- (12.47*(math.sin(4*((((2*math.pi)*res['DoY'])/366)+4.8718)))))\
/ 60
# Compute inverse relative distance factor (Distance between Earth and Sun)
res['sol_r'] = 1.0 / (1.0 - 9.464e-4 * math.sin(res['DoY']) \
- 0.01671 * math.cos(res['DoY']) \
- 1.489e-4 * math.cos(2.0 * res['DoY']) \
- 2.917e-5 * math.sin(3.0 * res['DoY']) \
- 3.438e-4 * math.cos(4.0 * res['DoY'])) ** 2
# Compute solar declination ################################################
res['sol_d'] = (math.asin(0.39785 * (math.sin(((278.97 \
+ (0.9856 * res['DoY'])) + (1.9165 \
* (math.sin((356.6 + (0.9856 * res['DoY'])) \
* (math.pi / 180))))) * (math.pi / 180)))) * 180) / math.pi
# Compute time of solar noon ###########################################
res['sol_n'] = ((12 + dst_off) - (res['eqt'] / 60)) \
- ((tz_off_deg - opt.lon) / 15)
# Compute solar zenith angle in DEG ####################################
res['sol_z'] = math.acos(((math.sin(opt.lat * (math.pi / 180))) \
* (math.sin(res['sol_d'] * (math.pi / 180)))) \
+ (((math.cos(opt.lat * ((math.pi / 180)))) \
* (math.cos(res['sol_d'] * (math.pi / 180)))) \
* (math.cos((res['ToD'] - res['sol_n']) \
* (math.pi /12))))) * (180/math.pi)
# A solar zenith angle value of > 90 usually indicates that the sun has set
# (from observer's perspective at the given location for this computation).
# However, in extreme latitudes, valid values over 90 may occur. If you live
# in such a place and happen to stumble upon this code, please report back
# when you use it so we can find a better fix for this than the follwing hack.
# Unfortunately, if we don't fail safely here, we are confronted with some
# nasty division by zero business further on, so...
if res['sol_z'] > 90:
output (opt, res)
sys.exit (0)
# Barometric pressure at site ##############################################
# (this should be replaced by the real measured value) in kPa
if opt.at_p:
# Real value given, convert hPa to kPa
opt.at_p = opt.at_p / 10
else:
# Estimate Pressure from given altitude
opt.at_p = math.pow(((288 - (0.0065 * (opt.alt - 0))) / 288), \
(9.80665 / (0.0065 * 287))) * 101.325
# Estimate air vapor pressure in kPa #######################################
res['at_vp'] = (0.61121 * math.exp((17.502 * opt.at_t) \
/ (240.97 + opt.at_t))) \
* (opt.at_h / 100)
# Extraterrestrial radiation in W/m2 #######################################
res['ETR'] = (opt.sc * res['sol_r']) \
* (math.cos(res['sol_z'] * (math.pi / 180)))
# Precipitable water in the atmosphere in mm ###############################
res['at_pw'] = ((0.14 * res['at_vp']) * opt.at_p) + 2.1
# Clearness index for direct beam radiation [unitless] #####################
res['CIDBR'] = 0.98 * (math.exp(((-0.00146 * opt.at_p) \
/ (opt.at_tc * (math.sin((90 - res['sol_z']) \
* (math.pi / 180))))) - (0.075 * (math.pow((res['at_pw'] \
/ (math.sin((90 - res['sol_z']) * (math.pi / 180)))),0.4)))))
# Transmissivity index for diffuse radiation [unitless] ####################
if (res['CIDBR'] > 0.15):
res['TIDR'] = 0.35 - (0.36 * res['CIDBR'])
else:
res['TIDR'] = 0.18 + (0.82 * res['CIDBR'])
# Model Estimated Shortwave Radiation (W/m2) ###############################
res['RSO'] = (res['CIDBR'] + res['TIDR']) * res['ETR']
# Estimate Theoretical Max. Power Output (Panel at nominal Efficiency) #####
res['pv_max'] = (res['RSO'] * opt.pv_a) / 100 * opt.pv_e
# Estimate conversion loss due to module temperature #######################
res['pv_l'] = (opt.pv_t-25 ) * opt.pv_tc
res['pv_lp'] = (res['pv_max'] / 100) * res['pv_l']
# Estimate conversion loss due to module age
res['pv_la'] = res['pv_max'] - (res['pv_max'] * opt.pv_ac)
# Estimate final System Power output
res['pv_out'] = res['pv_max'] - res['pv_la'] - res['pv_lp']
output (opt, res)
################################################################################
if __name__ == '__main__':
rc = main()
sys.exit (rc)
Installation
This should work on any operating system with Python 2.7 installed. Other python versions haven't been tested yet.
You can either clone the whole repo with documentation with
$ git clone https://github.com/apollo-ng/UCSSPM.git $ cd UCSSPM
or just download the script itself
$ wget https://raw.githubusercontent.com/apollo-ng/UCSSPM/master/ucsspm.py
Usage Example
$ ./ucsspm.py -v -pv_t 16 -at_t 9.3 -at_p 945.5 -at_h 81 --------+-------------------------------------------------------- UCSSPM | Clear-Sky Prediction for 2014-11-15 @ 13:31:36 --------+-------------------------------------------------------- Solar Constant : 1361.0 kW/m² @ 1AU Atmospheric turbidity coefficient : 0.95 ----------------------------------------------------------------- Equation of time : 15.6165056158 min Inverse relative distance factor : 1.00277104587 Sun declination : -18.2528587° Solar Noon : 11.7397249064 Barometric Pressure at site : 94.55 kPa Estimated Vapor Pressure at site : 0.948698993906 kPa Estimated Extraterrestrial Radiation : 456.410564923 W/m² Estimated precipitable water in Atmosphere : 14.6579285823 mm Clearness index for direct beam radiation : 0.451609480011 Transmissivity index for diffuse radiation : 0.187420587196 ----------------------------------------------------------------- Estimated Max. global solar radiation (Rs) : 291.7 W/m² ----------------------------------------------------------------- Optimum Elevation of PV-Panel : 70.5° Estimated Max. Clear-Sky PV-Power Output : 97.4 W @ 20% Peff PV-Panel temperature (16.0 °C) compensation + 3.1 W / 3.1% PV-Panel aging loss - 1.9 W ----------------------------------------------------------------- Compensated Max. Clear-Sky PV-Power Output : 98.5 W
Development / Sources / Issue-Tracking
Anyone interested is of course also invited to download the software and play/use/verify/optimize as well. Feedback, PR's and everything else that might increase precision/usability are always welcome:
In the Wild
If you're using the UCSSPM in your application too, let us know.
Roadmap
- Integrate long-term simulation/reference data into VFCC [DONE]
- Refactor into a python lib to be used either standalone or linked into python code [NEXT]
- Create a pip package for that lib